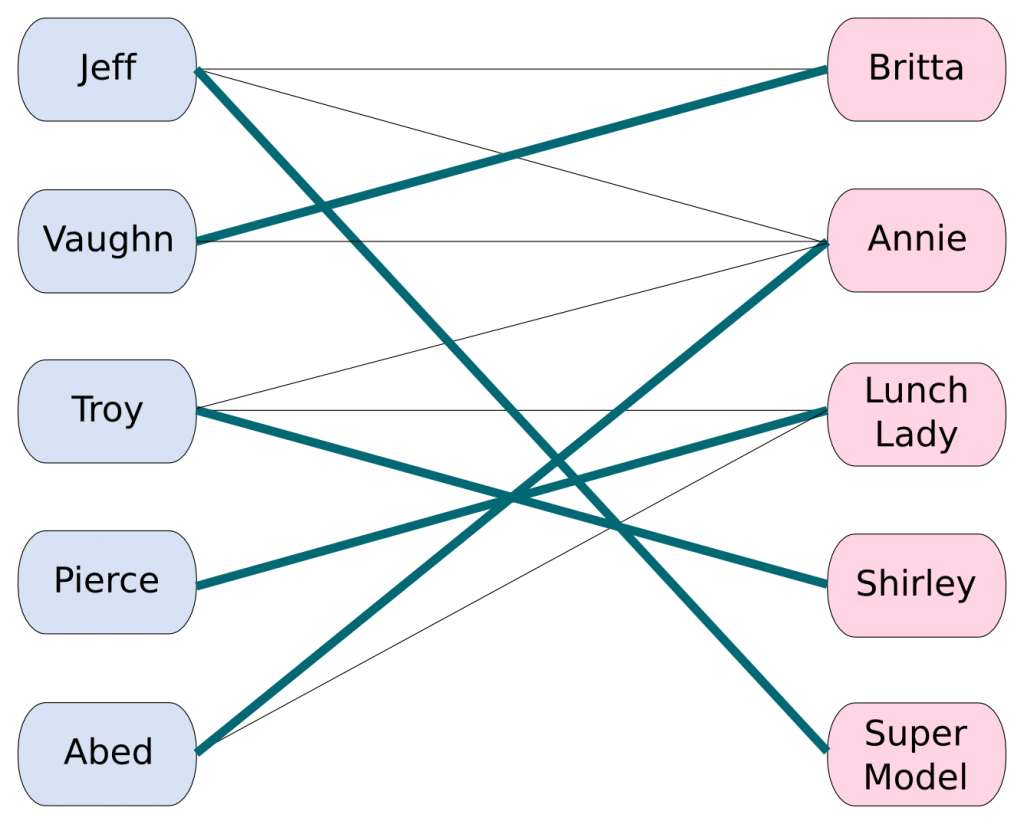
Задача. Пусть есть \(n\) мальчиков и \(m\) девочек. Про каждого мальчика и про каждую девочку известно, с кем они не против танцевать. Нужно составить как можно больше пар, в которых партнёры хотят танцевать друг с другом.

Формализуем эту задачу, представив мальчиков и девочек как вершины в двудольном графе, рёбрами которого будет отношение «могут танцевать вместе».
Паросочетанием \(M\) называется набор попарно несмежных рёбер графа (иными словами, любой вершине графа должно быть инцидентно не более одного ребра из \(M\)).
Все вершины, у которых есть смежное ребро из паросочетания (т.е. которые имеют степень ровно один в подграфе, образованном \(M\)), назовём насыщенными этим паросочетанием.
Мощностью паросочетания назовём количество рёбер в нём. Наибольшим (максимальным) паросочетанием назовём паросочетание, мощность которого максимальна среди всех возможных паросочетаний в данном графе, а совершенным — где все вершины левой доли им насыщенны.
Паросочетания можно искать в любых графах, однако этот алгоритм неприятно кодить, и он работает за \(O(n^3)\), так что сегодня мы сфокусируемся только на двудольных графах. Будем в дальнейшем обозначать левую долю графа как \(L\), а правую долю как \(R\).
Цепью длины \(k\) назовём некоторый простой путь (т.е. не содержащий повторяющихся вершин или рёбер), содержащий ровно \(k\) рёбер.
Чередующейся цепью относительно некоторого паросочетания назовём простой путь длины \(k\) в которой рёбра поочередно принадлежат/не принадлежат паросочетанию.
Увеличивающей цепью относительно некоторого паросочетания назовём чередующуюся цепь, у которой начальная и конечная вершины не принадлежат паросочетанию.

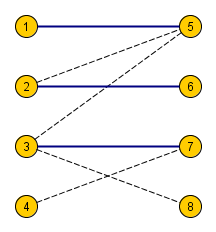
Здесь красными помечены вершины паросочетания, а в графе есть увеличивающая цепь: \(1 \to 8 \to 4 \to 6 \to 3 \to 7\).
Зачем нужны увеличивающие цепи? Оказывается, можно с их помощью увеличивать паросочетание на единицу (отсюда и название). Можно взять такой путь и провести чередование — убрать из паросочетания все рёбра, принадлежащие цепи, и, наоборот, добавить все остальные. Всего в увеличивающей цепи нечетное число рёбер, а первое и последнее были не в паросочетании. Значит, мощность паросочетания увеличилась ровно на единицу.
В примере добавятся синие рёбра \((1, 8)\), \((3, 7)\) и \((4, 6)\), а удалятся красные \((3, 6)\) и \((4, 8)\). С ребром \((2, 5)\) ничего не случится — оно не в увеличивающей цепи. Таким образом, размер паросочетания увеличится на единицу.
Алгоритм Куна в этом и заключается — будем искать увеличивающую цепь, пока ищется, и проводить чередование в ней. Увеличивающие цепи удобны тем, что их легко искать: можно просто запустить поиск пути из произвольной свободной вершины из левой доли в какую-нибудь свободную вершину правой доли в том же графе, но в котором из правой доли можно идти только по рёбрам паросочетания (то есть у вершин правой доли будет либо одно ребро, либо ноль). Это можно делать как угодно (для упражнения автор рекомендует явно строить такой граф, искать путь и явно проводить чередования), однако устоялась эффективная реализация в виде dfs на 20 строчек кода, приведённая ниже.
const int maxn;
vector<int> g[maxn]; // будем хранить только рёбра из левой доли в правую
int mt[maxn]; // с какой вершиной сматчена вершина правой доли (-1, если ни с какой)
bool used[maxn]; // вспомогательный массив для поиска пути dfs-ом
// dfs возвращает, можно ли найти путь из вершины v
// в какую-нибудь вершину правой доли
// если можно, то ещё и проводит чередование
bool dfs(int v) {
if (used[v])
return false;
used[v] = true;
for (int u : g[v]) {
// если вершина свободна, то можно сразу с ней соединиться
// если она занята, то с ней можно соединиться только тогда,
// когда из её текущей пары можно найти какую-нибудь другую вершину
if (mt[u] == -1 || dfs(mt[u])) {
mt[u] = v;
return true;
}
}
return false;
}
// где-то в main:
memset(mt, -1, sizeof mt);
for (int i = 0; i < n; i++) {
memset(used, 0, sizeof mt);
if (dfs(i))
cnt++;
}Для доказательства алгоритма нам будет достаточно ещё доказать, что если увеличивающие цепи уже не ищутся, то паросочетание в принципе нельзя увеличить.
Теорема (Бержа). Паросочетание без увеличивающих цепей является максимальным.
Доказательство проведём от противного: пусть есть два паросочетания вершин \(|A| \leq |B|\), и для \(A\) нет увеличивающих путей, и покажем, как найти этот путь и увеличить \(A\) на единицу.
Раскрасим ребра из паросочетания, соответствующего \(A\) в красный цвет, \(B\) — в синий, а ребра из обоих паросочетаний — в пурпурный. Рассмотрим граф из только красных и синих ребер. Любая компонента связности в нём представляет собой либо путь, либо цикл, состоящий из чередующихся красных и синих ребер. В любом цикле будет равное число красных и синих рёбер, а так как всего синих рёбер больше, то должен существовать путь, начинающийся и оканчивающийся синим ребром — он и будет увеличивающей цепью для \(A\), а значит \(A\) не оптимальное, и мы получили противоречие.
Такой алгоритм ровно \(n\) раз ищет увеличивающий путь, каждый раз просматривая не более \(m\) рёбер, а значит работает за \(O(nm)\).
Что примечательно, его можно не бояться запускать на ограничениях и побольше (\(n, m \approx 10^4\)), потому что для него есть мощные неасимптотические оптимизации:
Eго можно жадно инициализировать (просто заранее пройтись по вершинам левой доли и сматчить их со свободной вершиной правой, если она есть).
Можно не заполнять нулями на каждой итерации массив used, а использовать следующий трюк: хранить в нём вместо булева флага версию последнего изменения, а конкретно – номер итерации, на которой это значение стало true. Если этот номер меньше текущего номера итерации, то мы можем воспринимать это значение как false. В каком-то смысле это позволяет эмулировать очищение массива за константу.
Очень часто граф приходит из какой-то другой задачи, природа которой накладывает ограничения на его вид. Например, в задачах на решетках (когда есть двумерный массив, и соседние клетки связаны друг с другом) граф двудольный, но степень каждой вершины маленькая, и граф имеет очень специфичную структуру, и на нём алгоритм Куна работает быстрее, чем ожидается из формулы \(n \times m\). Контрпримеры в таких задачах на самом деле почти всегда можно сгенерировать, но авторы редко так заморачиваются.
Вообще говоря, увлекаться ускорением алгоритма Куна не стоит — существует более асимптотически быстрый алгоритм. Задача нахождения максимального паросочетания — частный случай задачи о максимальном потоке, и если применить алгоритм Диница к двудольным графам с единичной пропускной способностью, то выясняется, что работать он будет за \(O(m \sqrt n)\).
Сводить задачи к поиску максимального паросочетания обычно не очень трудно, но в некоторых случаях самому додуматься сложно. Разберём одну такую известную задачу. Дан ориентированный ациклический граф \(G\) (англ. directed acyclic graph). Требуется покрыть его наименьшим числом путей, то есть найти наименьшее множество простых путей, где каждая вершина принадлежит ровно одному пути.
Построим соответствующие изначальному графу \(G\) два двудольных графа \(H\) и \(\overline{H}\) следующим образом:
Если мы рассмотрим любой путь \(v_1, v_2, \ldots, v_k\) в исходном графе \(G\), то в графе \(\overline{H}\) ему будет соответствовать путь \(a_{v_1}, b_{v_2}, a_{v_2}, b_{v_3}, \ldots, a_{v_{k-1}}, b_{v_k}\). Обратное тоже верно: любой путь, начинающийся в левой доле \(\overline{H}\) и заканчивающийся в правой будет соответствовать какому-то пути в \(G\).
Итак, есть взаимно однозначное соответствие между путями в \(G\) и путями \(\overline{H}\), идущими из левой доли в правую. Заметим, что любой такой путь в \(\overline{H}\) — это паросочетание в \(H\) (напомним, это \(\overline{H}\) без обратных рёбер). Получается, любому пути из \(G\) можно поставить в соответствие паросочетание в \(H\), и наоборот. Более того, непересекающимся путям в \(G\) соответствуют непересекающиеся паросочетания в \(H\).
Заметим, что если есть \(p\) непересекающихся путей, покрывающих все \(n\) вершин графа, то они вместе содержат \(r = n - p\) рёбер. Отсюда получаем, что чтобы минимизировать число путей \(p\), мы должны максимизировать число рёбер \(r\) в них.
Мы теперь можем свести задачу к нахождению максимального паросочетания в двудольном графе \(H\). После нахождения этого паросочетания мы должны преобразовать его в набор путей в \(G\). Это делается тривиальным алгоритмом: возьмем \(a_1\), посмотрим, с какой \(b_k\) она соединена, посмотрим на \(a_k\) и так далее. Некоторые вершины могут остаться ненасыщенными — в таком случае в ответ надо добавить пути нулевой длины из каждой из этих вершин.
Лемма Холла (или: теорема о свадьбах) — очень удобный критерий в задачах, где нужно проверить, что паросочетание существует, но при этом не требуется строить его явно.
Лемма Холла. Полное паросочетание существует тогда и только тогда, когда любая группа вершин левой доли соединена с не меньшим количеством вершин правой доли.
Доказательство. В одну сторону понятно — если совершенное паросочетание есть, то для любого подмножества вершин левой доли можно взять вершины правой, соединенные с ним паросочетанием.
В другую сложнее — нужно воспользоваться индукцией. Будем доказывать, что если паросочетание не полное, то можно в таком графе найти увеличивающую цепь, и с её помощью увеличить паросочетание на единицу.
База индукции: одна вершина из \(L\), которая по условию соединена с хотя бы одной вершиной из \(R\).
Индукционный переход: пусть после \(k < n\) шагов построено паросочетание \(M\). Докажем, что в \(M\) можно добавить вершину \(v\) из \(L\), не насыщенную паросочетанием.
Рассмотрим множество вершин \(H\) — все вершины, достижимые из \(x\), если можно ходить из правой доли в левую только по рёбрам паросочетания, а из левой в правую — по любым (мы такой граф по сути строим, когда ищем увеличивающую цепь в алгоритме Куна)
Тогда в \(H\) найдется вершина \(y\) из \(R\), не насыщенная паросочетанием. Иначе, если такой вершины нет, то получается, что если рассмотреть вершины \(H_L\) (вершины левой доли, насыщенные паросочетанием), то для них не будет выполнено условие, что \(|H_L| \leq |N(H_L)|\) (здесь \(N(X)\) — множество вершин, соединенным паросочетанием с \(X\)).
Тогда должен существовать путь из \(x\) в \(y\), и он будет увеличивающим для паросочетания \(M\), потому что из \(R\) в \(L\) мы всегда шли только по ребрам паросочетания. Проведя чередование вдоль этого пути, получим большее паросочетание, следовательно предположение индукции верно.
Задача. Дан граф. Назовем вершинным покрытием такое множество вершин, что каждое ребро графа инцидентно хотя бы одной вершине из множества. Необходимо найти вершинное покрытие наименьшего размера.
Следует заметить, что в общем случае это очень сложная задача, но для двудольных графов она имеет достаточно простое решение.
Теорема. \(\mid V_{min} \mid \le \mid M \mid\), где \(V_{min}\) — минимальное вершинное покрытие, а \(M\) — максимальное паросочетание.
Доказательство. \(\mid V_{min} \mid \ge \mid M \mid\), поскольку \(M\) — множество независимых ребер. Теперь приведем алгоритм, который строит вершинное покрытие размера \(\mid M \mid\). Очевидно, оно будет минимальным.
Алгоритм. Мысленно ориентируем ребра графа: ребра из \(M\) проведем из правой доли в левую, остальные — из левой в правую, после чего запустим обход в глубину из всех вершин левой доли, не включенных в \(M\).

Заметим, что граф разбился на несколько множеств: \(L^+, L^-, R^+, R^-\), где “плюсовые” множества — это множества посещенных в процессе обхода вершин. В графе такого вида не бывает ребер \(L^+ \rightarrow R^-\), \(L^- \leftarrow R^+\) по очевидным соображениям. Ребер \(L^+ \leftarrow R^-\) не бывает, потому что в противном случае паросочетание \(M\) не максимальное — его можно дополнить ребрами такого типа.
\[ L^- \cup R^+ = V_{min} \]
Понятно, что данное множество покроет все ребра. Осталось выяснить, почему \(L^- \cup R^+\). Это верно потому, что \(L^- \cup R^+\) покрывает все ребра \(M\) ровно один раз (ведь ребра \(L^- \rightarrow R^+\) не принадлежат \(M\)), а также потому, что в нем нет вершин, не принадлежащих \(M\) (для \(L^-\) это справедливо по определению, для \(R^+\) можно провести доказательство от противного с использованием чередующихся цепей).
Упражнение. Подумайте, как это можно применить к решению задачи о нахождении максимального независимого множества.
С весьма большой вероятностью матроиды вам никогда не пригодятся в школьных олимпиадах, однако, если вам совсем нечего делать, можете про них почитать.
Математика вообще занимается тем, что обобщает всякие объекты и старается формулировать все теоремы максимально абстрактно. Так, концепцию хороших подмножеств (паросочетаний) обобщает понятие матроида. Практическое применение — жадный алгоритм Радо-Эдмондса, который нужен для обоснования большого числа жадников, где нужно набрать какое-то подмножество минимального / максимального веса. Сам алгоритм максимально простой: давайте отсортируем эти объекты по весу и будем добавлять их в таком порядке в наше хорошее множество, если оно после добавления остается хорошим.
Применимо к паросочетаниям: пусть у вершин левой доли есть вес, и нам нужно набрать максимальное паросочетание минимального веса. Тогда выясняется, что можно просто отсортировать вершины левой доли по весу и пытаться в таком порядке добавлять их в паросочетание стандартным алгоритмом Куна.