Разреженная таблица¶
- Нужна для нахождения минимума на отрезке за $O(1)$ с препроцессингом за $O(n \log n)$ с малой константой.
- Обновления не поддерживает (static RMQ).
- Так как LCA эквивалентна RMQ, может быть применена в разных задачах на деревья.
- Её можно строить на ходу. Это может быть полезно при подсчете всяких динамик (см. последний Всерос).
- Требует $O(n \log n)$ памяти.
- Также можно считать, например, gcd на отрезке за сложность одного gcd, но в основном её используют для RMQ.
Определим разреженную таблицу как двумерный массив размера $n \times\log n$:
$$ t[i][k] = \min \{ a_i, a_{i+1}, \ldots, a_{i+2^k-1} \} $$Идея такая: считаем минимум на каждом отрезке длины $2^k$.
Такой массив можно посчитать за его размер: $t[i][k] = \min(t[i][k-1], t[i+2^{k-1}][k-1])$. Считать его можно как итерируясь как по i, так и по k, причём какой-то из этих вариантов в несколко раз быстрее из-за кэширования.
Имея таком массив, мы можем в принципе для любого отрезка быстро посчитать минимум на нём. Нужно заметить, что у любого отрезка имеется два отрезка длины степени двойки, которые пересекаются, и, главное, покрывают его и только его целиком. Значит, мы можем просто взять минимум из значений, которые соответствуют этим отрезкам.
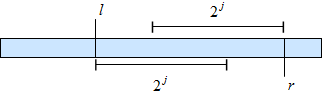
Последняя деталь: для того, чтобы константа на запрос стала настоящей, вместо функции log нужно предпосчитать массив округленных вниз логарифмов.
int a[maxn], lg[maxn], mx[maxn][logn];
int rmq (int l, int r) {
int t = lg[r-l+1];
return min(mx[l][t], mx[r-(1<<t)+1][t]);
}
// Это считается уже где-то в первых строчках main:
for (int l = 1; l < logn; l++)
for (int i = (1<<l); i < maxn; i++)
lg[i] = l;
for (int i = n-1; i >= 0; i--) {
mx[i][0] = a[i];
for (int l = 0; l < logn-1; l++)
mx[i][l+1] = max(mx[i][l], mx[i+(1<<l)][l]);
}
2d Static RMQ¶
Эту структуру тоже можно обобщить на большие размерности. Пусть мы хотим посчитать RMQ на подквадратах. Тогда вместо массива t[i][k] у нас будет массив t[i][j][k], в котором вместо минимума на отрезах будет храниться минимум на квадратах тех же степеней двоек. Получение минимума на произвольном квадрате тогда уже распадется на четыре минимума на квадратах длины $2^k$.
В общем же случае от нас просят минимум тоже на прямоугольниках. Тогда делаем предподсчет, аналогичный предыдущему случаю, только теперь тут будет $O(n \log^d n)$ памяти и времени на предподсчет.